It can be difficult to understand how efficient code can be based on just looking at it. Thankfully, people way smarter than me have figured out a way to understand how much time and space an algorithm takes based on the input.

Big O is a general way to measure the impact of your algorithm over space and time. Why do we need to know? Because our jobs as engineers is to find the best solution to any given problem. Engineering can be boiled down to the act of solving a problem that has never been solved before, or solving problems that have been solved before but more efficiently. Understanding Big O allows us to make informed decisions on what approach to take when solving problems. We can decide which algorithms to use based on how much time an space they would use based on what data the algorithm would be running on. Let's take a look at an example of a linear function, or O(n) (pronounced O of n) to make this easier to understand.

const arr = [1, 3, 5, 5, 4, 6, 12, ...];
const addAllArrayElements = (arr) =>{
	let sum = 0;
	for(let i=0; i < arr.length; i++){
		sum+=arr[i]
	}
	return sum;
}

Looking at the above example, we have a function that takes in an array of numbers and adds all of it's elements together, then returns the sum. We want to be able to predict roughly how long this operation will take. We can see that given an array of N elements, the for loop will run on each one. This gives us a runtime of O(n) as the function grows linearly with it's input. You could of course argue that assigning the new value to the sum variable takes time as well, and you'd be right, but in Big O computation we drop constants (in regards to computer science).

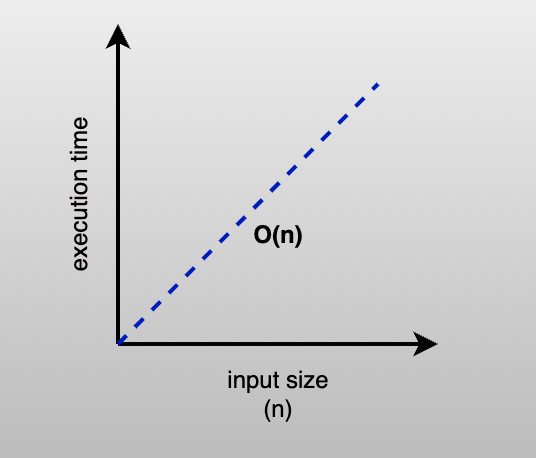
As you can see with the figure above, the execution time grows linearly with the size of the input. So if we know we are working with a small array, this approach makes sense, but as the size of our input grows or if we are unsure of how large the input will be, we may want to take a different approach.

While the linear time complexity is relatively easy to understand, there are of course other forms of complexity. So how do we recognize the different levels of complexity? One way to calculate it is to essentially look for loops. Loops will be your greatest indicator of time complexity. Let's take a look at another function.

const arr = [1, 3, 5, 5, 4, 6, 12, ...];
const addAllArrayElementsTwice = (arr) =>{
	let sum = 0;
	for(let i=0; i < arr.length; i++){
		sum+=arr[i]
	}
	for(let i=0; i < arr.length; i++){
		sum+=arr[i]
	}
	return sum;
}

If we had a linear complexity O(n) with one for loop, what would the complexity be here? If you said O(2n) congratulate yourself quickly but then relax because you are both right and wrong. Remember to drop the constants, in this case being 2, giving us still a complexity of O(n). A good tip would be to try to think of a function as a whole process. Let's take a look at another example.

const arr = [1, 3, 5, 5, 4, 6, 12, ...];
const addAllArrayElementsTwice = (arr) =>{
	let sum = 0;
	for(let i=0; i < arr.length; i++){
		sum+=arr[i]
		for(let j=0; j < arr.length; j++){
			sum+=arr[j]
		}
	}
	return sum;
}

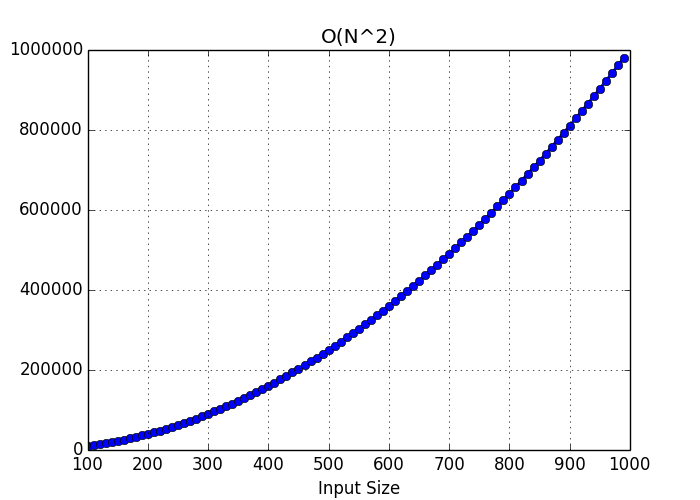
Here we have a function that loops through the array, adds the value to sum, and then for each element being added, we loop through the entire array again and add every element to the sum. This would be a runtime of O(n^2) or O of n squared. The same concept is true if we added another nested array to give us a run time of O(n^3) and so on.

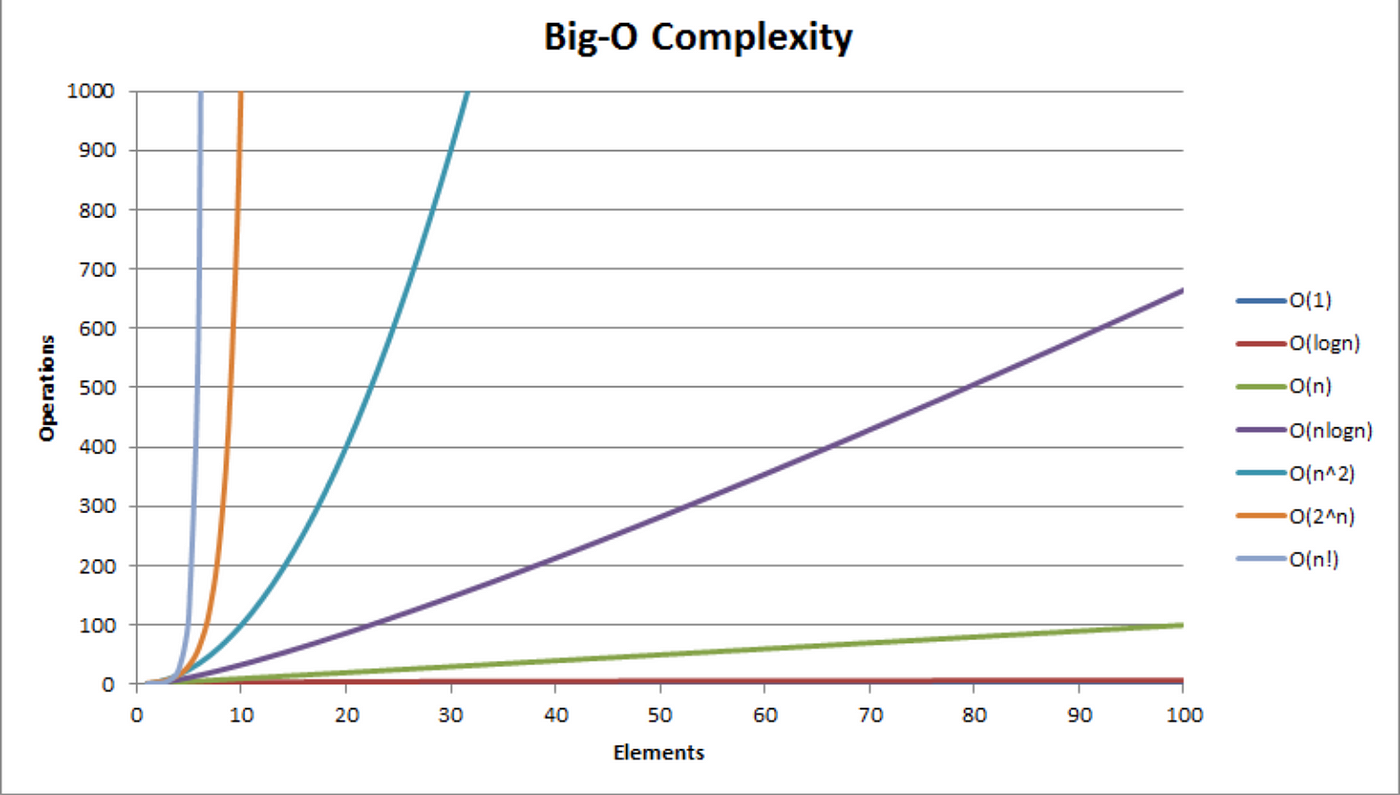
There are also other important runtimes you will need to know, such as O(n log n) and O(log n), but we will discuss those more as we learn about sorting algorithms. regardless, here is a quick picture to illustrate different complexities. If you think of it as the complexities being slower the more we move to the left, you can start to understand how the size of the input dictates the runtime.